| February 2026 | ||||||
|---|---|---|---|---|---|---|
| Sun | Mon | Tue | Wed | Thu | Fri | Sat |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| November | ||||||
time to move! Antville is a symatic community but I'm...
Post is THE company which implemented SOA the first time,...
Hypothesis: Since infrastucture code is not part of the domain...
this time It's the content, stupid http://www.joost.com/home?playNow=33l83ke#id=33l83ke
interface. I'm sceptical http://news.cnet.com/8301-17939_109-10065136-2.html
gives to the Pattern Movement Look what I've found: A...
Alexander—The pattern language that we began creating in the 1970s...
hill in the morning mist. Nasim Taleb explains the...
Roland Kofler's Blog on Software Engineering on

Hierarchical structure and the prediction of missing links in networks
I need to study this to understand how you could classify the dependency graph of a proliferated legacy architecture.
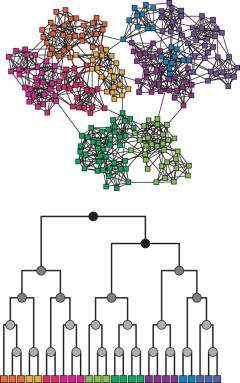 Networks have in recent years emerged as an invaluable tool for describing and quantifying complex systems in many branches of science (1–3). Recent studies suggest that networks often exhibit hierarchical organization, where vertices divide into groups that further subdivide into groups of groups, and so forth over multiple scales. In many cases these groups are found to correspond to known functional units, such as ecological niches in food webs, modules in biochemical networks (protein interaction networks, metabolic networks, or genetic regulatory networks), or communities in social networks (4–7). Here we present a general technique for inferring hierarchical structure from network data and demonstrate that the existence of hierarchy can simultaneously explain and quantitatively reproduce many commonly observed topological properties of networks, such as right-skewed degree distributions, high clustering coefficients, and short path lengths. We further show that knowledge of hierarchical structure can be used to predict missing connections in partially known networks with high accuracy, and for more general networkstructures than competing techniques (8). Taken together, our results suggest that hierarchy is a central organizing principle of complex networks, capable of offering insight into many network phenomena.
www-personal.umich.edu
Networks have in recent years emerged as an invaluable tool for describing and quantifying complex systems in many branches of science (1–3). Recent studies suggest that networks often exhibit hierarchical organization, where vertices divide into groups that further subdivide into groups of groups, and so forth over multiple scales. In many cases these groups are found to correspond to known functional units, such as ecological niches in food webs, modules in biochemical networks (protein interaction networks, metabolic networks, or genetic regulatory networks), or communities in social networks (4–7). Here we present a general technique for inferring hierarchical structure from network data and demonstrate that the existence of hierarchy can simultaneously explain and quantitatively reproduce many commonly observed topological properties of networks, such as right-skewed degree distributions, high clustering coefficients, and short path lengths. We further show that knowledge of hierarchical structure can be used to predict missing connections in partially known networks with high accuracy, and for more general networkstructures than competing techniques (8). Taken together, our results suggest that hierarchy is a central organizing principle of complex networks, capable of offering insight into many network phenomena.
www-personal.umich.edu
